Welcome to the TorchPhysics Tutorial Page!
The tutorial is split into two sections. First, a first-step tutorial is suited for beginners of TorchPhysics and physics-informed learning. Second, an in-depth tutorial gives insight into the diverse functionalities TorchPhysics provides, which enables the consideration of more complex problems. For example, problems in which more complicated geometries are to be considered, or even time-dependent domains. Last but not least, we list some examples, which further simplify the dive into TorchPhysics and other methods such as Deep Operator Networks3,4 (DeepONets) or the Deep Ritz method2.
First Steps - PINNs in TorchPhysics
For the first steps in TorchPhysics, we provide two parts, which differ in the complexity of the considered partial or ordinary differential equation (PDE, ODE). If you are familiar with PDEs and Python, you can also skip Part A) and move on to Part B) without losing any information.
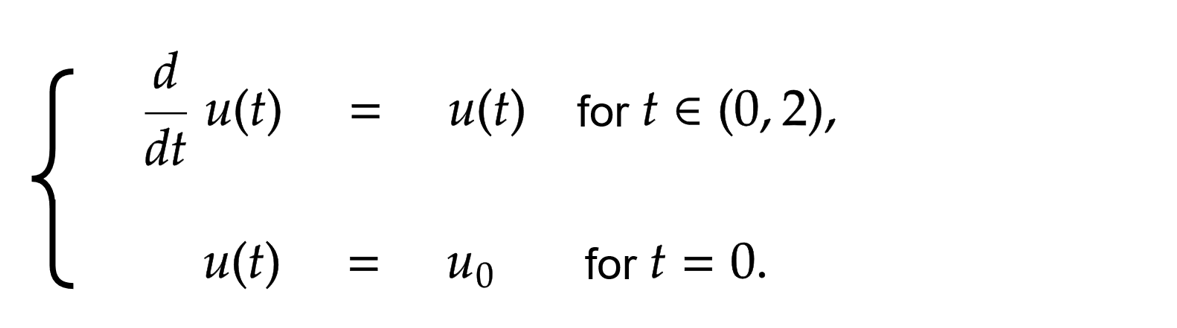
Part A) One of the simplest examples for the beginning is learning the exponential function, which solves the ODE depicted on the right. Click here to open the Jupyter Notebook. It contains:
Short recall of Physics-Informed Neural Networks1 (PINNs);
Step-by-step guide for implementation in TorchPhysics;
- Visualization of the learned solution.
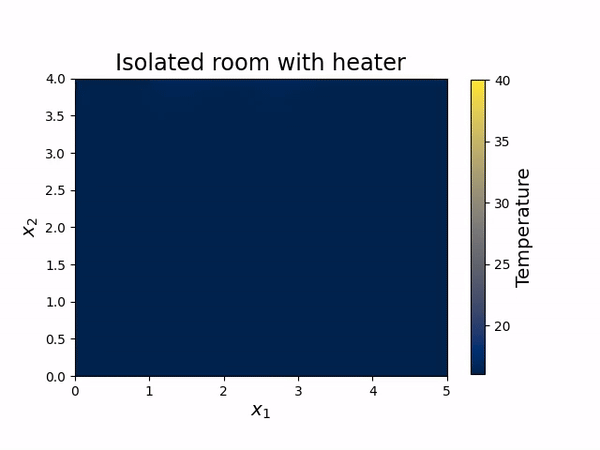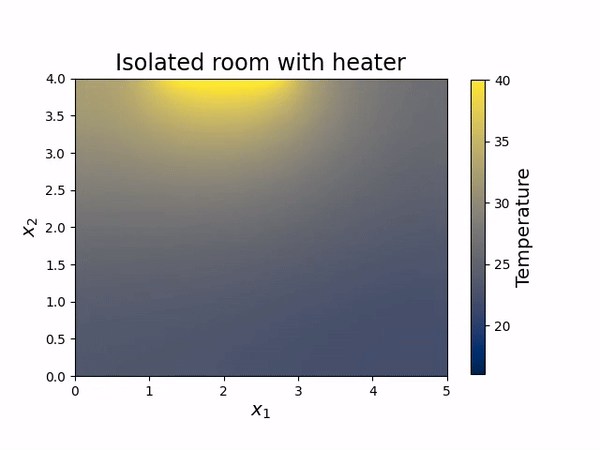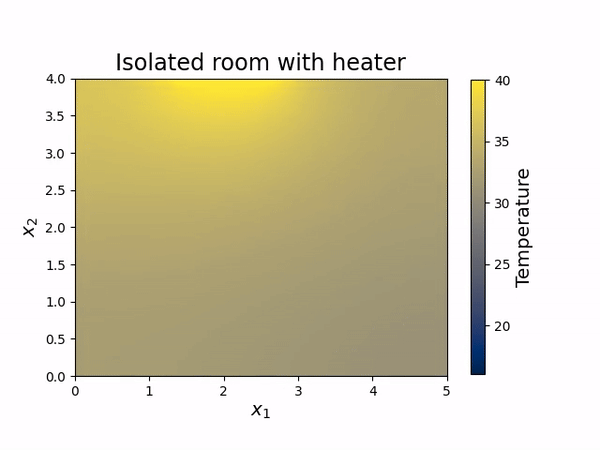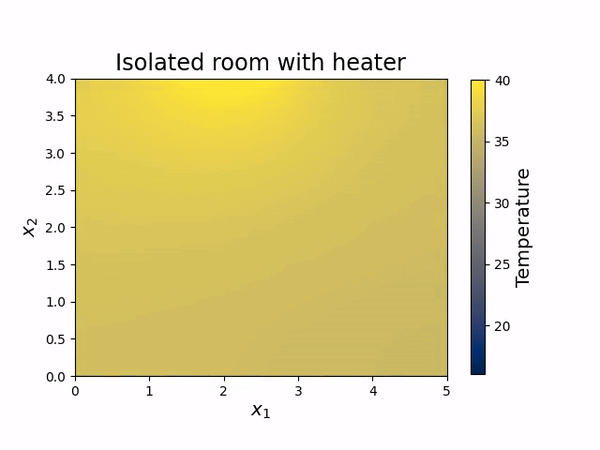
Part B) Time-dependent, two-dimensional heat equation is solved for a perfectly isolated room with a heater turned on (animation on the right). Click here to open the Jupyter Notebook. It contains:
Short recall of Physics-Informed Neural Networks1 (PINNs);
Step-by-step guide for implementation in TorchPhysics;
- Realization of Dirichlet and Neumann conditions;
- Visualization using TorchPhysics utilities, but also manually with Matplotlib.
PINNs can also be used for learning parameter-dependent PDEs: Solving the PDE above for different speeds of the heater reaching its final temperature is considered within this notebook.
In-depth Tutorial - Building Blocks of TorchPhysics
TorchPhysics provides lots of functionality that simplifies the implementation of more complex problems. For example, it could be desirable to
- consider more complex domains, e.g., domains changing over time;
- use different sampling strategies on domains, e.g., adaptive sampling;
- include complex PyTorch models into TorchPhysics;
- combine physics-informed with data-driven Deep Learning.
The in-depth tutorial provides more extensive insights into the structure of TorchPhysics, required for tackling more complex tasks.
Further Examples - PINNs, Deep Ritz Method, DeepONets
There are further examples with detailed explanations available:
- PINNs applied to 2D Poisson equation, comparison to analytic solution;
- Deep Ritz method which is applicable if a PDE can be described by some energy functional (e.g. for elliptic PDEs);
- Deep Operator Networks3,4 (DeepONets) are also available. For a beginner-friendly tutorial and a short recall of DeepONets click here. Therein, a DeepONet is trained physics-informed. Further, DeepONets can also be trained data-driven in TorchPhysics. DeepONets fall under the category of Operator Learning, i.e., a single network is used for solving a PDE for many different parameter functions.
- Inverse problems (parameter identification) are tackled with PINNs or DeepONets.
References
[1] Raissi, Perdikaris und Karniadakis, “Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations”, 2019 [2] Weinan E and Bing Yu, "The Deep Ritz method: A deep learning-based numerical algorithm for solving variational problems", 2017 [3] Lu, Jin and Karniadakis, “DeepONet: Learning nonlinear operators for identifying differential equations based on the universal approximation theorem of operators”, 2020 [4] Wang, Wang and Perdikaris, “Learning the solution operator of parametric partial differential equations with physics-informed DeepOnets”, 2021 |